Las funciones trigonométricas son relaciones matemáticas entre los lados de un triángulo rectángulo. Estas son:

• Seno (\(\sin\)): razón entre el cateto opuesto y la hipotenusa.


• Coseno (\(\cos\)): razón entre el cateto adyacente y la hipotenusa.


• Tangente (\(\tan\)): razón entre el cateto opuesto y el cateto adyacente.


• Cotangente (\(\cot\)): inversa de la tangente, es decir, \( \cot \theta = \frac{1}{\tan \theta} \).


• Secante (\(\sec\)): inversa del coseno, \( \sec \theta = \frac{1}{\cos \theta} \).


• Cosecante (\(\csc\)): inversa del seno, \( \csc \theta = \frac{1}{\sin \theta} \).

Seno (\(\sin\))

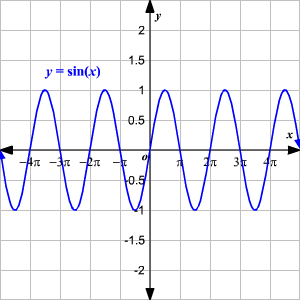
Coseno (\(\cos\))

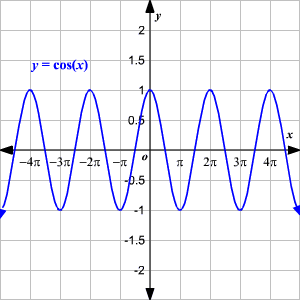
Tangente (\(\tan\))

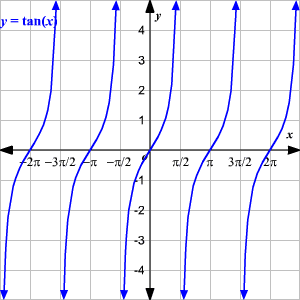
Secante (\(\sec\))

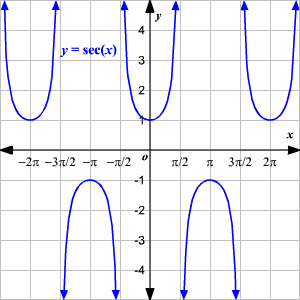
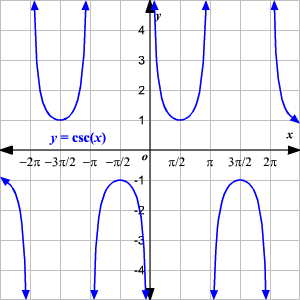
Cosecante (\(\csc\))

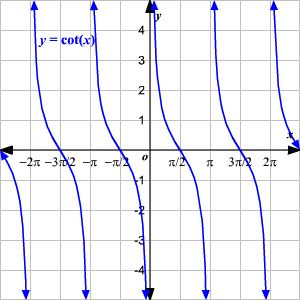
Cotangente (\(\cot\))

En muchos problemas de trigonometría, nos encontramos con ángulos que no son agudos (es decir, mayores de 90 grados o incluso negativos). Para simplificar cálculos y trabajar con valores conocidos, utilizamos identidades trigonométricas para convertir estos ángulos en su equivalente dentro del primer cuadrante.

Por ejemplo:

• \(\sin(150^\circ) = \sin(180^\circ - 150^\circ) = \sin(30^\circ)\)
• \(\cos(225^\circ) = -\cos(45^\circ)\)

¿Qué encontrarás en esta página?

• En la sección Funciones, aprenderás cómo transformar ángulos mayores de 90° en términos de ángulos agudos.



• En la sección Calculadora, podrás convertir cualquier ángulo en su equivalente agudo y obtener sus valores trigonométricos.



• En la sección Contáctanos, podrás enviarnos mensaje por si surge alguna duda